Função Sobrejetora
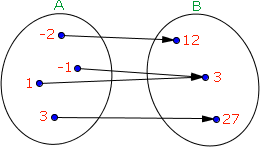
Vamos analisar o diagrama de flechas ao lado:
Como sabemos o conjunto A é o domínio da função e o conjunto B é o seu contradomínio.
É do nosso conhecimento que o conjunto imagem é o conjunto formado por todos os elementos do contradomínio que estão associados a pelo menos um elemento do domínio e neste nosso exemplo, todos os elementos de B estão associados a pelo menos um elemento de A, logo nesta função o contradomínio é igual ao conjunto imagem.
Classificamos como sobrejetora as funções que possuem o contradomínio igual ao conjunto imagem.
Note que em uma função sobrejetora não existem elementos no contradomínio que não estão flechados por algum elemento do domínio.
Nesta função de exemplo temos:
Domínio: D(f) = { -2, -1, 1, 3 }
Contradomínio: CD(f) = { 12, 3, 27 }
Conjunto Imagem: Im(f) = { 12, 3, 27 }
Esta função é definida por:
Substituindo a variável independente x, de 3x2, por qualquer elemento de A, iremos obter o elemento de B ao qual ele está associado, isto é, obteremos f(x).
Do que será explicado a seguir, poderemos concluir que embora esta função seja sobrejetora, ela não é uma função injetora.
Função Injetora
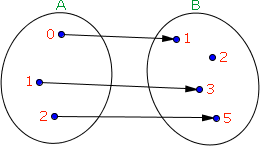
Vejamos agora este outro diagrama de flechas:
Podemos notar que nem todos os elementos de B estão associados aos elementos de A, isto é, nesta função o conjunto imagem difere docontradomínio, portanto esta não é uma função sobrejetora.
Além disto podemos notar que esta função tem uma outra característica distinta da função anterior.
Veja que não há nenhum elemento em B que está associado a mais de um elemento de A, ou seja, não há em Bqualquer elemento com mais de uma flechada. Em outras palavras não há mais de um elemento distinto de A com a mesma imagem em B.
Nesta função temos:
Domínio: D(f) = { 0, 1, 2 }
Contradomínio: CD(f) = { 1, 2, 3, 5 }
Conjunto Imagem: Im(f) = { 1, 3, 5 }
Definimos esta função por:
Veja que não há no D(f) qualquer elemento que substituindo x em 2x + 1, nos permita obter o elemento 2 doCD(f), isto é, o elemento 2 do CD(f) não é elemento da Im(f).
Função Bijetora
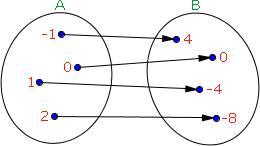
Na explicação do último tipo de função vamos analisar este outro diagrama de flechas:
Do explicado até aqui concluímos que este é o diagrama de umafunção sobrejetora, pois não há elementos em B que não foram flechados.
Concluímos também que esta é uma função injetora, já que todos os elementos de B recebem uma única flechada.
Esta função tem:
Domínio: D(f) = { -1, 0, 1, 2 }
Contradomínio: CD(f) = { 4, 0, -4, -8 }
Conjunto Imagem: Im(f) = { 4, 0, -4, -8 }
Esta função é definida por:
Ao substituirmos x em -4x, por cada um dos elementos de A, iremos encontrar os respectivos elementos de B, sem que sobrem elementos em CD(f) e sem que haja mais de um elemento do D(f) com a mesma Im(f).
Funções que como esta são tanto sobrejetora, quanto injetora, são classificadas como funções bijetoras.




